Built-In Abstract Functions
ISL and ASL have the following built-in abstract functions.
;; Natural (Natural -> X) -> (listof X)
;; produces (list (f 0) ... (f (- n 1)))
(define (build-list n f) ...)
;; (X -> boolean) (listof X) -> (listof X)
;; produce a list from all those items on lox for which p holds
(define (filter p lox) ...)
;; (X -> Y) (listof X) -> (listof Y)
;; produce a list by applying f to each item on lox
;; that is, (map f (list x-1 ... x-n)) = (list (f x-1) ... (f x-n))
(define (map f lox) ...)
;; (X -> boolean) (listof X) -> boolean
;; produce true if p produces true for every element of lox
(define (andmap p lox) ...)
;; (X -> boolean) (listof X) -> boolean
;; produce true if p produces true for some element of lox
(define (ormap p lox) ...)
;; (X Y -> Y) Y (listof X) -> Y
;; (foldr f base (list x-1 ... x-n)) = (f x-1 ... (f x-n base))
(define (foldr f base lox) ...)
;; (X Y -> Y) Y (listof X) -> Y
;; (foldl f base (list x-1 ... x-n)) = (f x-n ... (f x-1 base))
(define (foldl f base lox) ...)
;;=======================Q1=====================================
(require spd/tags)
;; Consider the following data definitions:
(@htdd Course)
(define-struct course (code number))
;; Course is (make-course String Natural)
;; interp. a course with a subject code,
;; and a course number.
(define C1 (make-course "CPSC" 110))
(define C2 (make-course "MATH" 101))
(define C3 (make-course "ANTH" 201))
(define C4 (make-course "CPSC" 121))
(define C5 (make-course "PHIL" 154))
(define C6 (make-course "SPAN" 240))
(@htdd Student)
(define-struct student (name courses))
;; Student is (make-student String (listof Course))
;; interp. a student with a name and
;; a list of courses they are enrolled in
(define S1 (make-student "Simon" (list C1 C2 C3)))
(define S2 (make-student "Ahmed" (list C2 C3)))
(define S3 (make-student "Ziyou" (list C3 C4 C5)))
(define S4 (make-student "Beth" (list C2 C3 C5 C6)))
(define S5 (make-student "Ally" (list C1 C2 C3 C4)))
(define S6 (make-student "Jesse" (list C2 C3 C6)))
(define LOS1 (list S1 S2 S3 S4))
(define LOS2 (list S2 S3 S4 S5))
(define LOS3 (list S2 S4 S6))
;;
;; Design a function called messages that consumes a subject code (string),
;; a message string, and a list of students. It should produce a list of
;; messages for all the students who are enrolled in at least one course in
;; that subject.
;;
;; The function definition must use built-in abstract functions wherever
;; appropriate. Any solution that includes the (listof X) template will not be
;; graded. So for example:
;;
;; (messages "CPSC" "are you free for brunch on 4/26?" LOS1)
;;
;; must produce:
;;
;; (list "Simon are you free for brunch on 4/26?"
;; "Ziyou are you free for brunch on 4/26?")
;;
;;
;;
(@htdf messages) ;; START YOUR FUNCTION DESIGN BELOW HERE.
(define (messages major msg los)
(local [(define (fn2 course)
(string=? (course-code course) major))
(define (fn1 s)
(ormap fn2 (student-courses s)))
(define (fn3 s)
(string-append (student-name s) msg))]
(map fn3 (filter fn1 los))))
;; lambda version
(define (messages major msg los)
(map (lambda (s)
(string-append (student-name s) msg))
(filter (lambda (s)
(ormap (lambda (course)
(string=? (course-code course) major))
(student-courses s)))
los)))
;;=======================Q2=====================================
; Part 1 Practice D: Design a TAIL RECURSIVE function that consumes a list of numbers *and produces*
; a count of the longest sequence of values found in a row that are equal.
;
; For example: The following list has 3 different sequences where numbers
; of equal value are found in row:
;
; (list 1 2 2 2 3 4 5 5 5 5 6 7 7 8)
;
; - there are three 2's in a row
; - there are four 5's in a row
; - there are two 7's in a row
;
; The longest sequence was the 5's, there were FOUR in a row,
; so the function should produce 4 given the list above.
;; (listof Number) -> Natural
;; produce the longest sequence of equal values found in a row in lon
(check-expect (longest-sequence empty) 0)
(check-expect (longest-sequence (list 1)) 1)
(check-expect (longest-sequence (list 9 8 8 8 7 7)) 3)
(check-expect (longest-sequence (list 1 2 2 2 3 3 3 3)) 4)
(define (longest-sequence lon0)
(local [;; rsf is Natural: longest sequence seen so far
;; prev is Number: value of previous (first lon) in lon
;; count: count of current sequence of matches
(define (fn-for-lon lon prev count rsf)
(cond [(empty? lon) (max count rsf)]
[else
(if (= (first lon) prev)
(fn-for-lon (rest lon) (first lon) (+ 1 count) rsf)
(fn-for-lon (rest lon) (first lon) 1 (max count rsf)))]))]
(fn-for-lon lon0 0 0 0)))
;;=======================Q3=====================================
;; Design a function called long-seq-list that consumes a list of natural
;; numbers and produces the longest sequence of consecutive numbers ignoring
;; duplicates. Note that two numbers are consecutive if adding 1 to the first
;; produces the second.
;;
;; For example:
;; (long-seq-list (list 1 1 1 2 2 5 5 5 7 8 8 9 15 19)) -> (list 7 8 9)
;;
;; Once we ignore duplicates, the longest sequence is clearly 7 8 9.
;;
;; You are guaranteed that the list is sorted and has at least one element.
;;
;; Your function MUST be tail-recursive.
;;
;; Finally remember that BSL/ISL/ASL have a primitive function called reverse
;; that given a list produces a list with the elements in reverse order.
(@htdf long-seq-list) ;START YOUR SOLUTION BELOW HERE
(define (long-seq-list lon0)
(local [;; rsf is (listof Natural): longest sequence seen so far
;; prev is Number: value of previous (first lon) in lon
;; curLongest is (listof Natural): current longest
(define (fn-for-lon lon prev curLongest rsf)
(cond [(empty? lon)
(if (> (length curLongest) (length rsf))
(reverse curLongest)
(reverse rsf))]
[else
(cond [(= (first lon) prev)
(fn-for-lon (rest lon) (first lon) curLongest rsf)]
[(= (add1 prev) (first lon))
(fn-for-lon (rest lon) (first lon) (cons (first lon) curLongest) rsf)]
[else
(fn-for-lon (rest lon)
(first lon)
(list (first lon))
(if (> (length curLongest) (length rsf))
curLongest
rsf))])]))]
(fn-for-lon (rest lon0) (first lon0) (list (first lon0)) empty)))


;;=======================Q4=====================================
You are given a collection of blocks all of the same width and depth but of
varying heights. All the heights are multiples of 1 inch. You are also given a
target height that is a multiple of 1 inch.
Your task is to design a program that will determine whether there exists some
subset of the blocks that can be stacked to the height of exactly the target height.
A collection of block heights and a target height is called a block problem.
For example, suppose you are given a collection of heights (list 1 5 3 3 4) and
a target of 10 as your block problem, then you can say that yes, there is a
subset of blocks that can be stacked to exactly height 10: the blocks 3 3 and 4.
But if you are given a collection of heights (list 2 2 2 2) and a target of 7,
then, no, there is no subset that can be stacked to attain the target height.
The way we want to solve the problem is by taking a block from the given collection,
and then determining whether there is a subset from the remaining blocks that can
be stacked to our NEW target height.
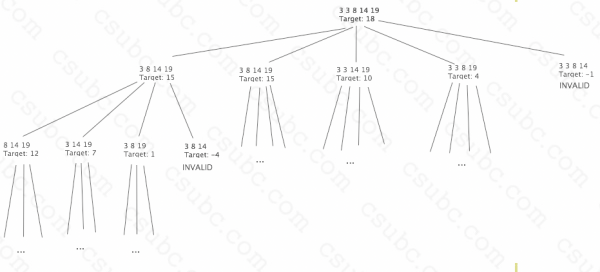
For example, if we were given the heights (list 3 3 8 14 19), and a target height of 18:
- We can take 3, and then solve for (list 3 8 14 19) with target 15
- We can take 3, and then solve for (list 3 8 14 19) with target 15
- We can take 8, and then solve for (list 3 3 14 19) with target 10
- We can take 14, and then solve for (list 3 3 8 19) with target 4
- We can take 19, and then solve for (list 3 3 8 14) with target -1
Note that one of our new problems has a negative target height. These problems
have no solution, as there is no way to stack block heights to a negative number.
So although we can generate these sorts of problems, these are not valid problems
and we should not continue solving them.
For all of the remaining (valid) problems, we can continue taking blocks until we get to
a target height of 0, or until there are no more blocks that we can take that produces
a valid problem. This results in something like this:

;;=======================Q5=====================================
; Problem 2
;
; In this problem set, you will design a program that will consume two strings (s1 and s2),
; and determine whether the letters in s1 are contained in s2. The letters must be in the
; same order, but other letters can be interleaved between those letters.
;
; For example,
;
; "abc" is contained in "xaxbxcx"
; "abc" is NOT contained in "axcxbx"
;
; You may have solved a similar practice problem using a 2 One Of table. Here, we are asking
; you to use a generative recursion approach. That is, we want to approach it by removing a letter
; from s2 and then determining whether s1 is contained in that new string.
;
; For example, if we wanted to see whether "el" is contained in "hello", we can generate the next
; possible scenerios:
; - whether "el" is contained in "ello" (by removing "h")
; - whether "el" is contained in "hllo" (by removing "e")
; - whether "el" is contained in "helo" (by removing "l")
; - whether "el" is contained in "helo" (by removing "l")
; - whether "el" is contained in "hell" (by removing "o")
;
; From there, we can continue removing letters from s2, generating the image below:
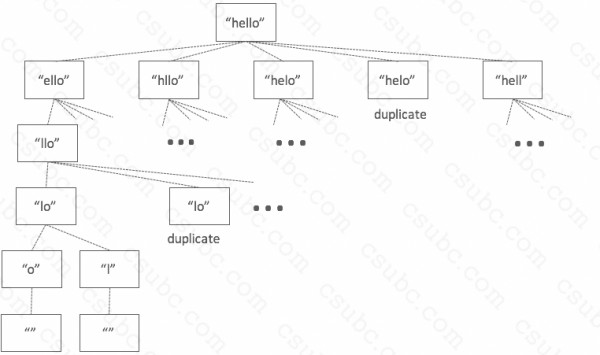
; There are instances where removing the letters results in the duplicate strings, like when we
; remove "l" to get "helo". In these cases, to avoid doing redundant work, we should filter out
; the duplicate strings before continuing with the search.
;
; NOTE: There are multiple ways to design this program (especially the helper functions).
; But remember to carefully follow the design recipes -- they are there to help you solve these
; more difficult problems!
