=====================3. two one of=======================
==========================Q1=======================
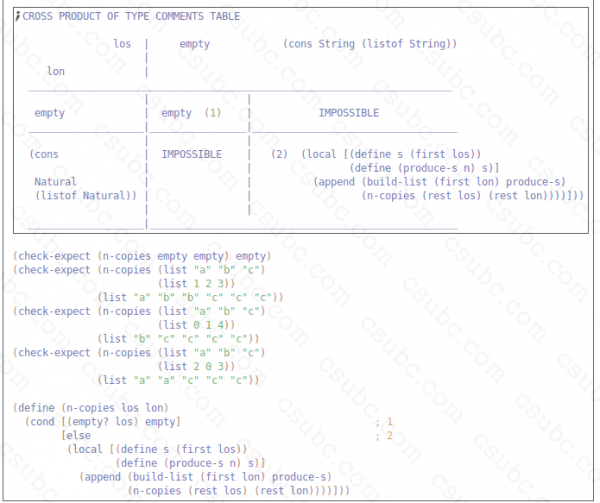
Design a function that consumes a (listof String) and a (listof Natural) and produces
a (listof String) that contains n copies of each String from the (listof String), where
n is the corresponding Natural in the (listof Natural). You must assume that the two
lists have the same length.
For example, (n-copies (list "a" "b" "c") produces (list "a" "b" "b" "c" "c" "c")
(list 1 2 3))
and (n-copies (list "a" "b" "c") produces (list "b" "c" "c" "c" "c")
(list 0 1 4))
and (n-copies (list "a" "b" "c") produces (list "a" "a" "c" "c" "c")
(list 2 0 3))
Treat this as a function operating on two complex data. You must show:
- signature, purpose, check-expects
- cross-product of types comment table with labeled axes and properly filled in cells
- complete function definition
- to show the correspondence between function and table you should number
each case in the function's cond, and number the corresponding table cell(s)
(if possible you must reduce the number of cases)
NOTE: No credit will be given to solutions that don't show a clear correspondence
to the cross-product of types comment table.
;; (listof String) (listof Natural) -> (listof String)
;; produces a list containing n copies of each String from los, where n is in the corresponding
;; position in lon
;; ASSUME: los and lon are the same length
===================================================
-
======================Q2===========================
We have weather data collected and stored in two lists:
-One list holds the temperature readings as numbers for each day in degrees celcius.
-The other list holds accuracy measures as Booleans for each day:
true if the corresponding temperature reading was accurate for the day, false if it wasn't.
Using the data definitions below, design a function that
takes a list of temperatures and a list of accuracy measures
and produces a list of only the accurate temperature readings.
If there are more temperature readings than accuracy measures,
the function should keep the extra temperature readings at the end of the result list.
If there are fewer temperature readings than accuracy measures
the function should ignore the extra accuracy measures.
Examples:
Calling the function with (list 2 -4.5 8.7) (list true false true),
only the 1st and 3rd readings are accurate,
therefore the function would produce (list 2 8.7)
Calling the function with (list 2 -4.5 8.7 9.2 33.1) (list true false),
only the 1st reading is accurate, the second is not and
the remaining 3 numbers in the list of temperatures are included,
therefore the function would produce (list 2 8.7 9.2 33.1)
Calling the function with (list 2 -4.5 8.7) (list false true true true true),
only the 2nd and 3rd readings are accurate and
the remaining 2 booleans in the list of accuracy measures are ignored,
therefore the function would produce (list -4.5 8.7)
Be sure to state any assumptions you are making and show your cross-product table.
;; ListOfNumber is one of:
;; - empty
;; - (cons Number ListOfNumber)
;; interp. a list of Numbers
(define LON0 empty)
(define LON3 (list -4.2 13.7 27.9))
(define (fn-for-lon lon)
(cond [(empty? lon) (...)]
[else
(... (first lon)
(fn-for-lon (rest lon)))]))
;; ListOfBoolean is one of:
;; - empty
;; - (cons Boolean ListOfBoolean)
;; interp. a list of Booleans
(define LOB0 empty)
(define LOB3 (list true false true))
(define (fn-for-lob lob)
(cond [(empty? lob) (...)]
[else
(... (first lob)
(fn-for-lob (rest lob)))]))

===================================================
-
=====================Q3===========================
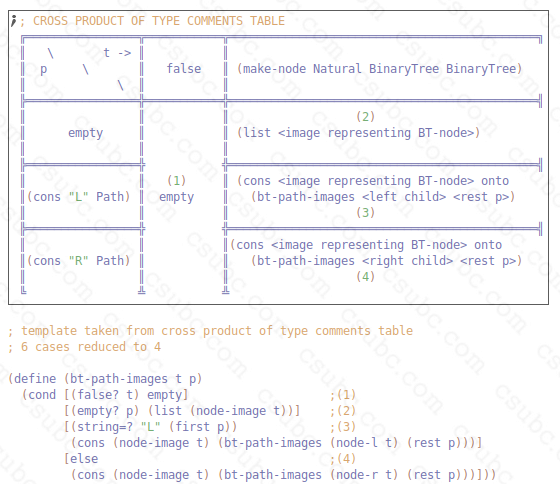
****
You are provided with a signature, purpose, stub, check-expects, and cross-product of
type comments table. Complete the function design, including origin of template comment.
You must reduce the cross-product of type comments table to the MINIMUM number of cases.
You must label each cell and corresponding cond Q/A pair in your function with a number.
NOTE: There is a helper function called node-image that you may use in your solution.
(require 2htdp/image)
(require spd/tags)
(define FONT-SIZE 14)
(define FONT-COLOR "black")
(@htdd BinaryTree)
(define-struct node (key l r))
;; BinaryTree is one of:
;; - false
;; - (make-node Natural BinaryTree BinaryTree)
;; interp. a binary tree, each node has a key and left/right children
(define BT0 false)
(define BT16 (make-node 16 false false))
(define BT40 (make-node 40 BT16 false))
(define BT45 (make-node 45 BT40 (make-node 80
(make-node 66 false false)
(make-node 98 false false))))
#;
(define (fn-for-bt bt)
(cond [(false? bt) (...)]
[else
(... (node-key bt)
(fn-for-bt (node-l bt))
(fn-for-bt (node-r bt)))]))
(@htdd Path)
;; Path is one of:
;; - empty
;; - (cons "L" Path)
;; - (cons "R" Path)
;; interp. A sequence of left and right 'turns' down through a BinaryTree.
;; (list "L" "R" "R") means take the left child of the root,
;; then the right child of that node, and the right child again.
(define P1 empty)
(define P2 (list "L" "R"))
#;
(define (fn-for-path p)
(cond [(empty? p) (...)]
[(string=? (first p) "L") (... (fn-for-path (rest p)))]
[(string=? (first p) "R") (... (fn-for-path (rest p)))]))
;; BinaryTree -> Image
;; produce an image representing the node of a BT
(check-expect (node-image false) empty-image)
(check-expect (node-image BT16) (overlay (text "16" FONT-SIZE FONT-COLOR)
(circle 16 "outline" "red")))
(check-expect (node-image BT40) (overlay (text "40" FONT-SIZE FONT-COLOR)
(circle 40 "outline" "red")))
; template from BinaryTree
(define (node-image bt)
(cond [(false? bt) empty-image]
[else
(overlay (text (number->string (node-key bt)) FONT-SIZE FONT-COLOR)
(circle (node-key bt) "outline" "red"))]))
;; BinaryTree Path -> (listof Image)
;; produce a list of images representing the path taken through t
(check-expect (bt-path-images false empty) empty)
(check-expect (bt-path-images false (cons "L" empty)) empty)
(check-expect (bt-path-images false (cons "R" empty)) empty)
(check-expect (bt-path-images BT16 empty)
(list (overlay (text "16" FONT-SIZE FONT-COLOR)
(circle 16 "outline" "red"))))
(check-expect (bt-path-images BT45 (cons "R" (cons "L" (cons "L" empty))))
(list (overlay (text "45" FONT-SIZE FONT-COLOR) (circle 45 "outline" "red"))
(overlay (text "80" FONT-SIZE FONT-COLOR) (circle 80 "outline" "red"))
(overlay (text "66" FONT-SIZE FONT-COLOR) (circle 66 "outline" "red"))))
;(define (bt-path-images t p) empty) ;stub
==================================================
-
=====================Q4===========================
Consider the below data definition for a Binary Tree. Design a function
that consumes two Binary Trees and determines if they are duplicate trees
(i.e. have exactly the same nodes in exactly the same positions).
Treat this as a function operating on two complex data. You must show:
- signature, purpose, and check-expects
- cross-product of types comment table with labeled axes and properly
filled in cells
- complete function definition
- to show the correspondence between function and table, you should number
each case in the function's cond, and number the corresponding table cell(s)
NOTE: No credit will be given to solutions that don't show a clear correspondence
to the cross-product of types comment table.
Note: Some sections only saw Binary Search Trees (BSTs). A Binary Tree
has the same structure as a BST but is not sorted (i.e. does not have the
invariant that requires all the keys in the left subtree to be less than
key and all the keys in the right subtree to be bigger than key.)
(@htdd BT)
(define-struct node (key val l r))
;; a BT (Binary Tree) is one of:
;; - false
;; - (make-node Integer String BT BT)
;; interp. false means no BT, or empty BT
;; key is the node key
;; val is the node val
;; l and r are left and right subtrees
(define BT0 false)
(define BT25 (make-node 25 "dog" false false))
(define BT40 (make-node 40 "cat" false (make-node 7 "alligator" false false)))
(define BT3 (make-node 3 "horse" BT25 BT40))
(define BT68
(make-node 68 "parrot"
(make-node 9 "snake" (make-node 99 "worm" false false) false)
(make-node 37 "mouse" false false)))
(define BT65
(make-node 65 "rabbit" BT3 BT68))

==================================================
-
======================Q5==========================
The depth of a binary tree at some node is described as the number of branches
needed to traverse from the root to get to that node.
For example, for this particular binary tree:
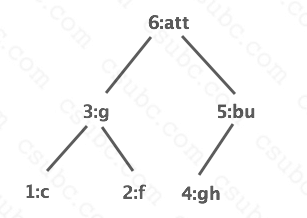
The root node is at depth 0. The node with key 3 has depth 1.
The node with key 5 also has depth 1. The nodes with keys 1, 2, and 4, have
depth of 2.
Design a function that consumes a natural number n and a binary tree
and produces all the keys of the nodes at depth n. We have provided the
data definitions for natural and binary tree below.
Treat this as a function operating on two complex data. You must show:
- signature, purpose, and check-expects
- cross-product of types comment table with labeled axes and properly
filled in cells
- complete function definition
- to show the correspondence between function and table, you should number
each case in the function's cond, and number the corresponding table cell(s)
(if possible, you must reduce the number of cases)
NOTE: No credit will be given to solutions that don't show a clear correspondence
to the cross-product of types comment table.
(require spd/tags)
(require 2htdp/image)
(@htdd Natural)
;; Natural is one of
;; - 0
;; - (add1 Natural)
;; interp. a natural number
(define N0 0)
(define N1 (add1 N0))
(define N2 (add1 N1))
#;
(define (fn-for-natural n)
(cond [(zero? n) (...)]
[else
(... n
(fn-for-natural (sub1 n)))]))
(@htdd Node)
(define-struct node (key val l r))
;; BT (Binary Tree) is one of:
;; - false
;; - (make-node Integer String BT BT)
;; interp. false means no BT, or empty BT
;; key is the node key
;; val is the node val
;; l and r are left and right subtrees
(define BT0 false)
(define BT1 (make-node 1 "c" false false))
(define BT2 (make-node 2 "f" false false))
(define BT3 (make-node 3 "g" BT1 BT2))
(define BT4 (make-node 4 "gh" false false))
(define BT5 (make-node 5 "bu" BT4 false))
(define BT6 (make-node 6 "att" BT3 BT5))
#;
(define (fn-for-bt bt)
(cond [(false? bt) ...]
[else
(... (node-key bt)
(node-val bt)
(fn-for-bt (node-l bt))
(fn-for-bt (node-r bt)))]))

==================================================